Integration Solving Integral With Complex Analysis Mathematics

Integration Solving Integral With Complex Analysis Mathematics This is known as the complex version of the fundamental theorem of calculus. theorem 4.2.1. let f(z) = f′ (z) be the derivative of a single valued complex function f(z) defined on a domain Ω ⊂ c. let c be any countour lying entirely in Ω with initial point z0 and final point z1. 8.5: complex integration. page id. russell herman. university of north carolina wilmington. we have introduced functions of a complex variable. we also established when functions are differentiable as complex functions, or holomorphic. in this chapter we will turn to integration in the complex plane.

Integration Properties Examples Formula Methods 1.3 complex integration and residue calculus 1.3.1 the cauchy integral formula theorem. (cauchy integral formula) let f(ξ) be analytic in a region r. let c ∼ 0 in r, so that c = ∂s, where s is a bounded region contained in r. let z be a point in s. then f(z) = 1 2πi z c f(ξ) ξ −z dξ. (1.31) proof: let cδ(z) be a small circle about z. 4. complex integration: cauchy integral theorem and cauchy integral formulas definite integral of a complex valued function of a real variable consider a complex valued function f(t) of a real variable t: f(t) = u(t) iv(t), which is assumed to be a piecewise continuous function defined in the closed interval a ≤ t ≤ b. Explanation: (5): apply (2) and (3) (6): the integrand is even; double the domain of integration and divide by 2. (7): write sin(θ) and cos(θ) in terms of eiθ. (8): substitute z =eiθ. (9): multiply numerator and denominator by z2. (10): residue at z = 0 is 1 y and the residue at z = y√ is − 1 y y(1−y) note that (8) is the final. Complex analysis is a basic tool in many mathematical theories. by itself and through some of these theories it also has a great many practical applications. there are a small number of far reaching theorems that we’ll explore in the rst part of the class. along the way, we’ll touch on some mathematical and engineering applications of.

Gaussian Integral 11 Complex Analysis Youtube Explanation: (5): apply (2) and (3) (6): the integrand is even; double the domain of integration and divide by 2. (7): write sin(θ) and cos(θ) in terms of eiθ. (8): substitute z =eiθ. (9): multiply numerator and denominator by z2. (10): residue at z = 0 is 1 y and the residue at z = y√ is − 1 y y(1−y) note that (8) is the final. Complex analysis is a basic tool in many mathematical theories. by itself and through some of these theories it also has a great many practical applications. there are a small number of far reaching theorems that we’ll explore in the rst part of the class. along the way, we’ll touch on some mathematical and engineering applications of. Contour integral. consider a contour c parametrized by z (t) = x (t) i y (t) for a ≤ t ≤ b. we define the integral of the complex function along c to be the complex number (1) ∫ c f (z) d z = ∫ a b f (z (t)) z ′ (t) d t. here we assume that f (z (t)) is piecewise continuous on the interval a ≤ t ≤ b and refer to the function f. Has animated versions of escher’s lithograph brought to life using the math ematics of complex analysis. •complex dynamics, e.g., the iconic mandelbrot set. see fig. 2. there are many other applications and beautiful connections of complex analysis to other areas of mathematics. (if you run across some interesting ones, please let me know!).

Complex Integration Lecture 2 How To Solve Complex Integral Contour integral. consider a contour c parametrized by z (t) = x (t) i y (t) for a ≤ t ≤ b. we define the integral of the complex function along c to be the complex number (1) ∫ c f (z) d z = ∫ a b f (z (t)) z ′ (t) d t. here we assume that f (z (t)) is piecewise continuous on the interval a ≤ t ≤ b and refer to the function f. Has animated versions of escher’s lithograph brought to life using the math ematics of complex analysis. •complex dynamics, e.g., the iconic mandelbrot set. see fig. 2. there are many other applications and beautiful connections of complex analysis to other areas of mathematics. (if you run across some interesting ones, please let me know!).
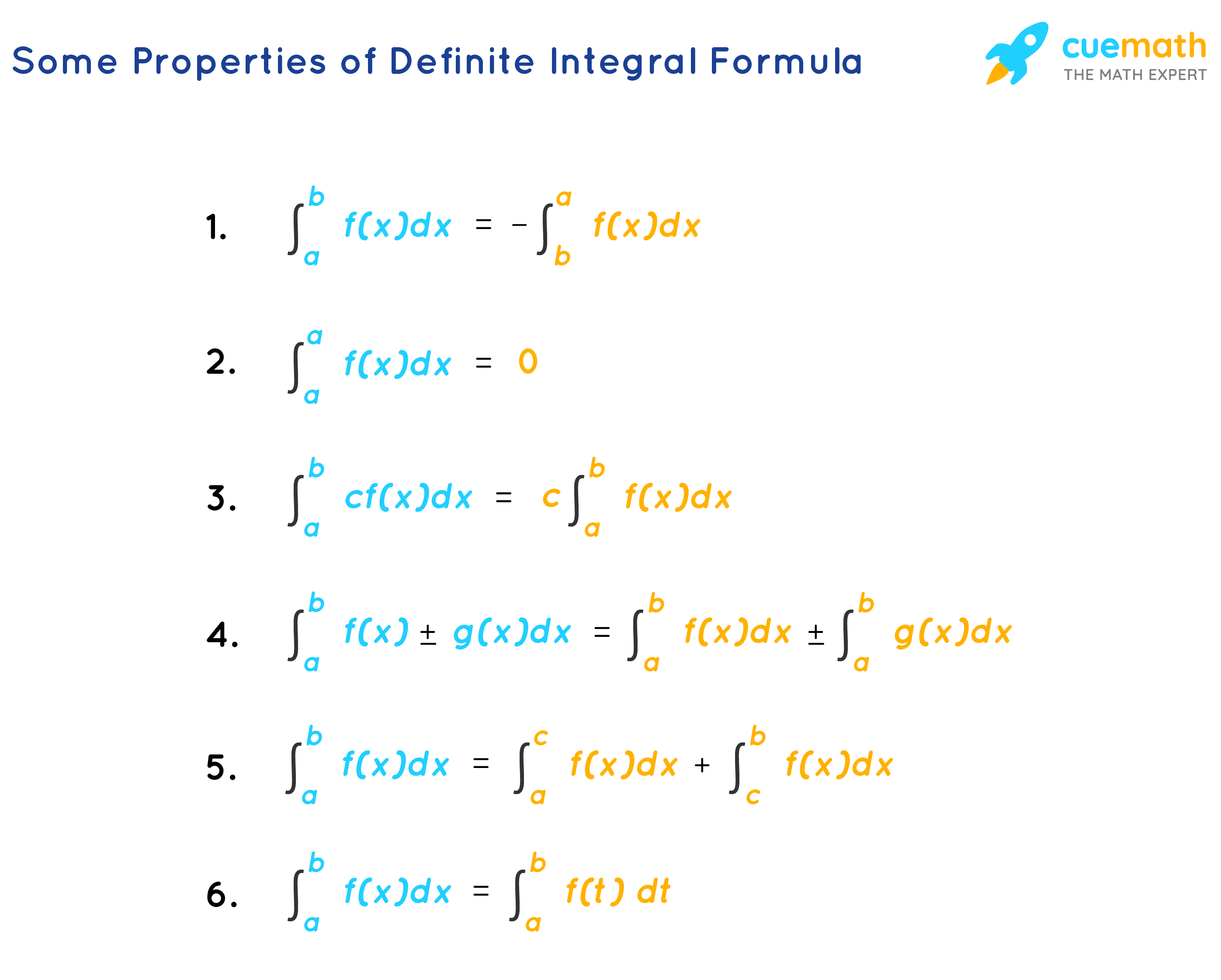
Definite Integral Formula Learn Formula To Calculate Definite Integral

Comments are closed.