Solved Hw Sec 5 5 Part 1 Substitution In The Indefinite Chegg

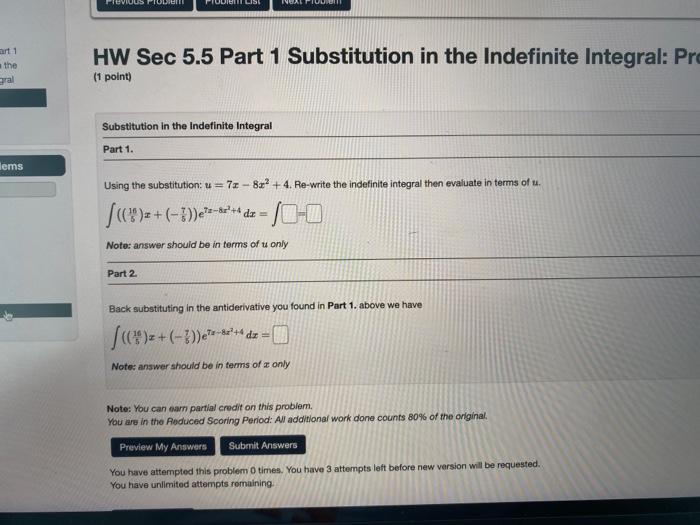
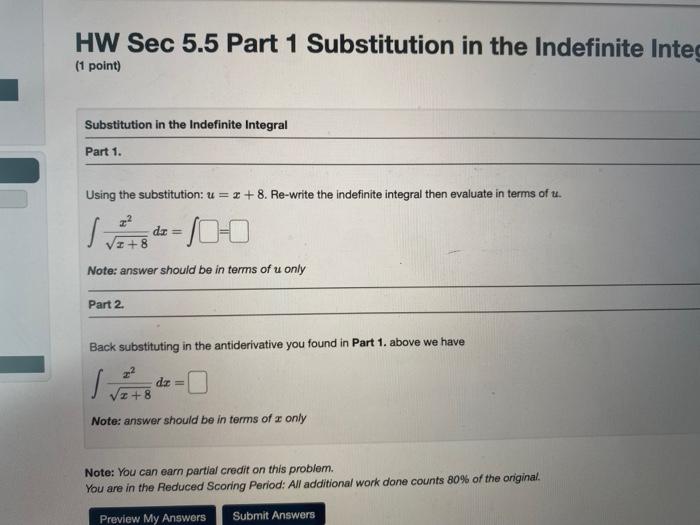
Solved Hw Sec 5 5 Part 1 Substitution In The Indefin Question: hw sec 5.5 part 1 substitution in the indefinite integral: pr (1 point) substitution in the indefinite integral part1. using the substitution: u=7x−8x2 4. re write the indefinite integral then evaluate in terms of u. ∫((165)x (−57))e7x−8x2 4dx=5 note: answer should be in terms of u only part 2. Step 1. hw sec 5.5 part 1 substitution in the indefinite integral: problem 5 (1 point) substitution in the indefinite integral part 1. using the substitution: u=x8. re write the indefinite integral then evaluate in terms of u. ∫ x7cos(x8)dx=∫ = note: answer should be in terms of u only part 2. back substituting in the antiderivative you.
Solved Hw Sec 5 5 Part 1 Substitution In The Inde Steps to u substitution. 1. pick 'u' so that the integral is easier. 1tip: this is usually the 'inside' of someting. 2. the derivative of u must be in the integrand. 3. transform integral of f (x)dx to integral of (u) (du) 4. solve the integral. 5 translate back to x or whatever variable you start with. Study guide substitution with indefinite integrals. problem solving strategy: integration by substitution. look carefully at the integrand and select an expression [latex]g(x)[ latex] within the integrand to set equal to [latex]u[ latex]. 5.1 approximating areas; 5.2 the definite integral; 5.3 the fundamental theorem of calculus; 5.4 integration formulas and the net change theorem; 5.5 substitution; 5.6 integrals involving exponential and logarithmic functions; 5.7 integrals resulting in inverse trigonometric functions. Rewrite the integral (equation 5.5.1) in terms of u: ∫(x2 − 3)3(2xdx) = ∫u3du. using the power rule for integrals, we have. ∫u3du = u4 4 c. substitute the original expression for x back into the solution: u4 4 c = (x2 − 3)4 4 c. we can generalize the procedure in the following problem solving strategy.
Solved Hw Sec 5 5 Part 1 Substitution In The Inde 5.1 approximating areas; 5.2 the definite integral; 5.3 the fundamental theorem of calculus; 5.4 integration formulas and the net change theorem; 5.5 substitution; 5.6 integrals involving exponential and logarithmic functions; 5.7 integrals resulting in inverse trigonometric functions. Rewrite the integral (equation 5.5.1) in terms of u: ∫(x2 − 3)3(2xdx) = ∫u3du. using the power rule for integrals, we have. ∫u3du = u4 4 c. substitute the original expression for x back into the solution: u4 4 c = (x2 − 3)4 4 c. we can generalize the procedure in the following problem solving strategy. The first step is to rewrite the function and simplify it so we can apply the power rule: ∫4 1√t(1 t)dt = ∫4 1t1 2(1 t)dt = ∫4 1(t1 2 t3 2)dt. now apply the power rule: ∫4 1(t1 2 t3 2)dt = (2 3t3 2 2 5t5 2)|4 1 = [2 3(4)3 2 2 5(4)5 2] − [2 3(1)3 2 2 5(1)5 2] = 256 15. exercise 5.5.1. A ∫ 3x 1 9x2 dx ∫ 3 x 1 9 x 2 d x show solution. in this case it looks like the substitution should be. b ∫ 3x (1 9x2)4 dx ∫ 3 x (1 9 x 2) 4 d x show solution. the substitution and differential work for this part are identical to the previous part. be careful to not just turn every integral of functions of the form of 1.

Solved Hw Sec 5 5 Part 1 Substitution In The Inde The first step is to rewrite the function and simplify it so we can apply the power rule: ∫4 1√t(1 t)dt = ∫4 1t1 2(1 t)dt = ∫4 1(t1 2 t3 2)dt. now apply the power rule: ∫4 1(t1 2 t3 2)dt = (2 3t3 2 2 5t5 2)|4 1 = [2 3(4)3 2 2 5(4)5 2] − [2 3(1)3 2 2 5(1)5 2] = 256 15. exercise 5.5.1. A ∫ 3x 1 9x2 dx ∫ 3 x 1 9 x 2 d x show solution. in this case it looks like the substitution should be. b ∫ 3x (1 9x2)4 dx ∫ 3 x (1 9 x 2) 4 d x show solution. the substitution and differential work for this part are identical to the previous part. be careful to not just turn every integral of functions of the form of 1.

Comments are closed.